Using osqp-eigen in MPC fashion
The problem is to develop a controller that allows a linear system to track a constant reference state . This kind of problem can be solved using a lot of different controller architectures, however in order to write a tutorial for osqp-eigen library the MPC approach will be chosen. Thus we have to find a controller low such that:
where , and are symmetric positive definite matrices; the states and the inputs have to be constrained between some lower and upper bounds and the reference state is
Convert MPC into a QP
First of all the MPC problem has to be casted to a standard QP problem.
where the hessian matrix is equal to
while the gradient vector is
The linear constraint matrix is
while the upper and the lower bound are
Since the osqp-eigen handles only QP problem this operation shall be done by the user. You can find the implementation of the following functions here.
castMPCToQPHessian(Q, R, mpcWindow, hessian); castMPCToQPGradient(Q, xRef, mpcWindow, gradient); castMPCToQPConstraintMatrix(a, b, mpcWindow, linearMatrix); castMPCToQPConstraintVectors(xMax, xMin, uMax, uMin, x0, mpcWindow, lowerBound, upperBound);
Solver initialization
Now you are able to use the OSQP solver. We first create an instance of the solver
// instantiate the solver OsqpEigen::Solver solver;
when the solver is instantiated the default settings are automatically loaded, however you can change each setting using the following function solver.settings()->set<Setting>() where set<Setting>() is a setter function. You can find the list of all the setter functions in the OsqpEigen:: class. For example you can use the warm start variables in the optimization problem by calling solver.settings()->setWarmStart(true);
Now you can set the data of the optimization problem (number of variables, number of constraints and so on)
solver.data()->setNumberOfVariables(numberOfVariable); solver.data()->setNumberOfConstraints(numberOfConstraints); if(!solver.data()->setHessianMatrix(hessian)) return 1; if(!solver.data()->setGradient(gradient)) return 1; if(!solver.data()->setLinearConstraintMatrix(linearMatrix)) return 1; if(!solver.data()->setLowerBound(lowerBound)) return 1; if(!solver.data()->setUpperBound(upperBound)) return 1;
The setter functions return True in case of success and False otherwise.
Now you are able to initialize the solver. All data and settings will be stored inside the osqp struct and the optimization problem will be initialized. if(!solver.initSolver()) return 1;
The optimization problem can be solved calling the following method if(solver.solveProblem() != OsqpEigen::ErrorExitFlag::NoError) return 1; and the solution can be easily got by calling the following method Eigen::VectorXd QPSolution = solver.getSolution();
If you need to update the bounds constraints and the gradient vector you can use the following methods:
OsqpEigen::to update both upper and lower bounds;Solver:: updateBounds OsqpEigen::to update the lower bound;Solver:: updateLowerBound OsqpEigen::to update the upper bound;Solver:: updateUpperBound OsqpEigen::to update the gradient vector.Solver:: updateGradient
Example
In the following the example of MPC controller is shown.
// osqp-eigen #include "OsqpEigen/OsqpEigen.h" // eigen #include <Eigen/Dense> #include <iostream> void setDynamicsMatrices(Eigen::Matrix<double, 12, 12>& a, Eigen::Matrix<double, 12, 4>& b) { a << 1., 0., 0., 0., 0., 0., 0.1, 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.1, 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.1, 0., 0., 0., 0.0488, 0., 0., 1., 0., 0., 0.0016, 0., 0., 0.0992, 0., 0., 0., -0.0488, 0., 0., 1., 0., 0., -0.0016, 0., 0., 0.0992, 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.0992, 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0.9734, 0., 0., 0., 0., 0., 0.0488, 0., 0., 0.9846, 0., 0., 0., -0.9734, 0., 0., 0., 0., 0., -0.0488, 0., 0., 0.9846, 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.9846; b << 0., -0.0726, 0., 0.0726, -0.0726, 0., 0.0726, 0., -0.0152, 0.0152, -0.0152, 0.0152, -0., -0.0006, -0., 0.0006, 0.0006, 0., -0.0006, 0.0000, 0.0106, 0.0106, 0.0106, 0.0106, 0, -1.4512, 0., 1.4512, -1.4512, 0., 1.4512, 0., -0.3049, 0.3049, -0.3049, 0.3049, -0., -0.0236, 0., 0.0236, 0.0236, 0., -0.0236, 0., 0.2107, 0.2107, 0.2107, 0.2107; } void setInequalityConstraints(Eigen::Matrix<double, 12, 1>& xMax, Eigen::Matrix<double, 12, 1>& xMin, Eigen::Matrix<double, 4, 1>& uMax, Eigen::Matrix<double, 4, 1>& uMin) { double u0 = 10.5916; // input inequality constraints uMin << 9.6 - u0, 9.6 - u0, 9.6 - u0, 9.6 - u0; uMax << 13 - u0, 13 - u0, 13 - u0, 13 - u0; // state inequality constraints xMin << -M_PI / 6, -M_PI / 6, -OsqpEigen::INFTY, -OsqpEigen::INFTY, -OsqpEigen::INFTY, -1., -OsqpEigen::INFTY, -OsqpEigen::INFTY, -OsqpEigen::INFTY, -OsqpEigen::INFTY, -OsqpEigen::INFTY, -OsqpEigen::INFTY; xMax << M_PI / 6, M_PI / 6, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY; } void setWeightMatrices(Eigen::DiagonalMatrix<double, 12>& Q, Eigen::DiagonalMatrix<double, 4>& R) { Q.diagonal() << 0, 0, 10., 10., 10., 10., 0, 0, 0, 5., 5., 5.; R.diagonal() << 0.1, 0.1, 0.1, 0.1; } void castMPCToQPHessian(const Eigen::DiagonalMatrix<double, 12>& Q, const Eigen::DiagonalMatrix<double, 4>& R, int mpcWindow, Eigen::SparseMatrix<double>& hessianMatrix) { hessianMatrix.resize(12 * (mpcWindow + 1) + 4 * mpcWindow, 12 * (mpcWindow + 1) + 4 * mpcWindow); // populate hessian matrix for (int i = 0; i < 12 * (mpcWindow + 1) + 4 * mpcWindow; i++) { if (i < 12 * (mpcWindow + 1)) { int posQ = i % 12; float value = Q.diagonal()[posQ]; if (value != 0) hessianMatrix.insert(i, i) = value; } else { int posR = i % 4; float value = R.diagonal()[posR]; if (value != 0) hessianMatrix.insert(i, i) = value; } } } void castMPCToQPGradient(const Eigen::DiagonalMatrix<double, 12>& Q, const Eigen::Matrix<double, 12, 1>& xRef, int mpcWindow, Eigen::VectorXd& gradient) { Eigen::Matrix<double, 12, 1> Qx_ref; Qx_ref = Q * (-xRef); // populate the gradient vector gradient = Eigen::VectorXd::Zero(12 * (mpcWindow + 1) + 4 * mpcWindow, 1); for (int i = 0; i < 12 * (mpcWindow + 1); i++) { int posQ = i % 12; float value = Qx_ref(posQ, 0); gradient(i, 0) = value; } } void castMPCToQPConstraintMatrix(const Eigen::Matrix<double, 12, 12>& dynamicMatrix, const Eigen::Matrix<double, 12, 4>& controlMatrix, int mpcWindow, Eigen::SparseMatrix<double>& constraintMatrix) { constraintMatrix.resize(12 * (mpcWindow + 1) + 12 * (mpcWindow + 1) + 4 * mpcWindow, 12 * (mpcWindow + 1) + 4 * mpcWindow); // populate linear constraint matrix for (int i = 0; i < 12 * (mpcWindow + 1); i++) { constraintMatrix.insert(i, i) = -1; } for (int i = 0; i < mpcWindow; i++) for (int j = 0; j < 12; j++) for (int k = 0; k < 12; k++) { float value = dynamicMatrix(j, k); if (value != 0) { constraintMatrix.insert(12 * (i + 1) + j, 12 * i + k) = value; } } for (int i = 0; i < mpcWindow; i++) for (int j = 0; j < 12; j++) for (int k = 0; k < 4; k++) { float value = controlMatrix(j, k); if (value != 0) { constraintMatrix.insert(12 * (i + 1) + j, 4 * i + k + 12 * (mpcWindow + 1)) = value; } } for (int i = 0; i < 12 * (mpcWindow + 1) + 4 * mpcWindow; i++) { constraintMatrix.insert(i + (mpcWindow + 1) * 12, i) = 1; } } void castMPCToQPConstraintVectors(const Eigen::Matrix<double, 12, 1>& xMax, const Eigen::Matrix<double, 12, 1>& xMin, const Eigen::Matrix<double, 4, 1>& uMax, const Eigen::Matrix<double, 4, 1>& uMin, const Eigen::Matrix<double, 12, 1>& x0, int mpcWindow, Eigen::VectorXd& lowerBound, Eigen::VectorXd& upperBound) { // evaluate the lower and the upper inequality vectors Eigen::VectorXd lowerInequality = Eigen::MatrixXd::Zero(12 * (mpcWindow + 1) + 4 * mpcWindow, 1); Eigen::VectorXd upperInequality = Eigen::MatrixXd::Zero(12 * (mpcWindow + 1) + 4 * mpcWindow, 1); for (int i = 0; i < mpcWindow + 1; i++) { lowerInequality.block(12 * i, 0, 12, 1) = xMin; upperInequality.block(12 * i, 0, 12, 1) = xMax; } for (int i = 0; i < mpcWindow; i++) { lowerInequality.block(4 * i + 12 * (mpcWindow + 1), 0, 4, 1) = uMin; upperInequality.block(4 * i + 12 * (mpcWindow + 1), 0, 4, 1) = uMax; } // evaluate the lower and the upper equality vectors Eigen::VectorXd lowerEquality = Eigen::MatrixXd::Zero(12 * (mpcWindow + 1), 1); Eigen::VectorXd upperEquality; lowerEquality.block(0, 0, 12, 1) = -x0; upperEquality = lowerEquality; lowerEquality = lowerEquality; // merge inequality and equality vectors lowerBound = Eigen::MatrixXd::Zero(2 * 12 * (mpcWindow + 1) + 4 * mpcWindow, 1); lowerBound << lowerEquality, lowerInequality; upperBound = Eigen::MatrixXd::Zero(2 * 12 * (mpcWindow + 1) + 4 * mpcWindow, 1); upperBound << upperEquality, upperInequality; } void updateConstraintVectors(const Eigen::Matrix<double, 12, 1>& x0, Eigen::VectorXd& lowerBound, Eigen::VectorXd& upperBound) { lowerBound.block(0, 0, 12, 1) = -x0; upperBound.block(0, 0, 12, 1) = -x0; } double getErrorNorm(const Eigen::Matrix<double, 12, 1>& x, const Eigen::Matrix<double, 12, 1>& xRef) { // evaluate the error Eigen::Matrix<double, 12, 1> error = x - xRef; // return the norm return error.norm(); } int main() { // set the preview window int mpcWindow = 20; // allocate the dynamics matrices Eigen::Matrix<double, 12, 12> a; Eigen::Matrix<double, 12, 4> b; // allocate the constraints vector Eigen::Matrix<double, 12, 1> xMax; Eigen::Matrix<double, 12, 1> xMin; Eigen::Matrix<double, 4, 1> uMax; Eigen::Matrix<double, 4, 1> uMin; // allocate the weight matrices Eigen::DiagonalMatrix<double, 12> Q; Eigen::DiagonalMatrix<double, 4> R; // allocate the initial and the reference state space Eigen::Matrix<double, 12, 1> x0; Eigen::Matrix<double, 12, 1> xRef; // allocate QP problem matrices and vectors Eigen::SparseMatrix<double> hessian; Eigen::VectorXd gradient; Eigen::SparseMatrix<double> linearMatrix; Eigen::VectorXd lowerBound; Eigen::VectorXd upperBound; // set the initial and the desired states x0 << 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0; xRef << 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0; // set MPC problem quantities setDynamicsMatrices(a, b); setInequalityConstraints(xMax, xMin, uMax, uMin); setWeightMatrices(Q, R); // cast the MPC problem as QP problem castMPCToQPHessian(Q, R, mpcWindow, hessian); castMPCToQPGradient(Q, xRef, mpcWindow, gradient); castMPCToQPConstraintMatrix(a, b, mpcWindow, linearMatrix); castMPCToQPConstraintVectors(xMax, xMin, uMax, uMin, x0, mpcWindow, lowerBound, upperBound); // instantiate the solver OsqpEigen::Solver solver; // settings // solver.settings()->setVerbosity(false); solver.settings()->setWarmStart(true); // set the initial data of the QP solver solver.data()->setNumberOfVariables(12 * (mpcWindow + 1) + 4 * mpcWindow); solver.data()->setNumberOfConstraints(2 * 12 * (mpcWindow + 1) + 4 * mpcWindow); if (!solver.data()->setHessianMatrix(hessian)) return 1; if (!solver.data()->setGradient(gradient)) return 1; if (!solver.data()->setLinearConstraintsMatrix(linearMatrix)) return 1; if (!solver.data()->setLowerBound(lowerBound)) return 1; if (!solver.data()->setUpperBound(upperBound)) return 1; // instantiate the solver if (!solver.initSolver()) return 1; // controller input and QPSolution vector Eigen::Vector4d ctr; Eigen::VectorXd QPSolution; // number of iteration steps int numberOfSteps = 50; for (int i = 0; i < numberOfSteps; i++) { // solve the QP problem if (solver.solveProblem() != OsqpEigen::ErrorExitFlag::NoError) return 1; // get the controller input QPSolution = solver.getSolution(); ctr = QPSolution.block(12 * (mpcWindow + 1), 0, 4, 1); // save data into file auto x0Data = x0.data(); // propagate the model x0 = a * x0 + b * ctr; // update the constraint bound updateConstraintVectors(x0, lowerBound, upperBound); if (!solver.updateBounds(lowerBound, upperBound)) return 1; } return 0; }
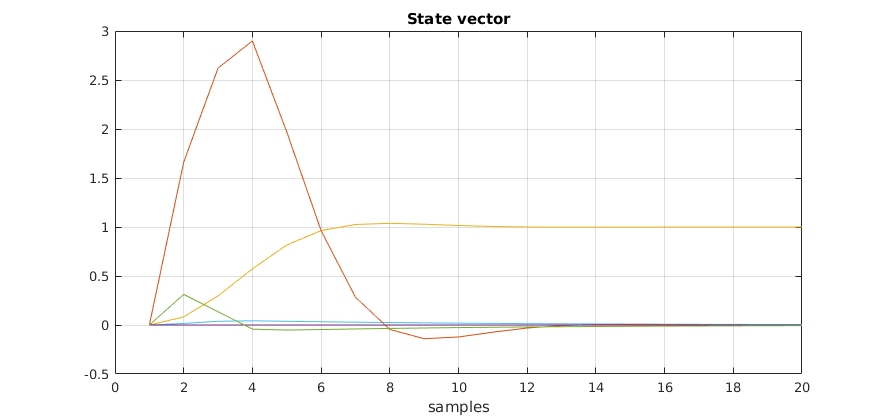
The example presented generates the following results